---- Księga Gości ----
Wpisz się... | Przeglądaj...
4.
TAUTOLOGIA RACHUNKU ZDAN -
jest to wylacznie prawdziwy schemat zdania
wyrazonego w jezyku rachunku zdan. O jego
prawdziwosci rozstrzygamy poprzez
podstawienie w miejsca zmiennych zdaniowych
jedynek (wartosci prawdy), oraz zer
(wartosci falszu), we wszystkich mozliwych
kombinacjach ( jest ich, jak pamietamy : 2n,
gdzie “n” jest liczba zmiennych zdaniowych).
Jej przeciwienstwo to KONTRTAUTOLOGIA,
ktora jest wylacznie falszywym schematem
zdania wyrazonego w jezyku rachunku zdan.
Widzisz, ze ostateczna wartosc
logiczna calego schematu, po przeprowadzeniu
wszystkich operacji, stanowia same jedynki.
Wiec nie pozostaje nam - teraz juz znawcom
logiki, nic innego, jak nazwac powyzszy
schemat tautologia.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 |
| Wystarczylo zanegowac drugi czlon
implikacji wystepujacej w schemacie tautologii
i zastapic sam glowny funktor rownowaznoscia
by uzyskac kontrtautologie ( podkreslone same
zera ). CWICZENIE 7 Czeka nas teraz "zabawa" ze sprawdzaniem tego czy schematy sa tautologia, kontrtautologia czy tez ani tym, ani tym... a)
Sposob postepowania jest
nastepujacy:
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Teraz, po zastapieniu glownego spojnika poprzedniego schematu z implikacji na rownowaznosc, nie otrzymalismy juz tautologii (podkreslone jedno zero), ani kontrtautologii (podkreslone trzy jedynki). Nasz schemat jest wiec najzwyklejszym ze schematow, nie dzierzacym szlachetnego miana jakim jest tautologia czy tez kontrtautologia. _____ c)
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
I oto naszym oczom ukazala sie w swej pelnej krasie kontrtautologia (podkreslone same zera, bedace wartosciami logicznymi glownego spojnika schematu - negacji, dla poszczegolnych kombinacji zerojedynkowych). _____ d)
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
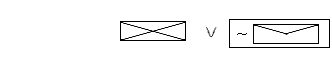 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
UWAGA ! Zerojedynkowa procedura sprawdzania tautologicznosci schematow logicznych moze byc skrocona za sprawa wspanialego umyslu ludzkiego, ktory to jest w stanie uproscic Czlowiekowi wszystko, co tylko do uproszczenia sie nadaje. Poprzez rozumne zanalizowanie schematu mozemy darowac sobie zmudne podstawianie do niego wszystkich kombinacji zmiennych skladowych (w przykladach “c” i “d” poprzedniego cwiczenia mielismy ich az 8, a ilez dopiero pracy byloby przy 16), czyniac to tylko z tymi wariantami, ktore z zalozenia moglyby powodowac jego nietautologicznosc.
Skomplikowane? Na pewno jeszcze tak, ale po wykonaniu kilku cwiczonek zobaczysz, ze nie bedzie Ci sie chcialo rozstawac z ta metoda do konca Twoich dni... oczywiscie tych z logika, jako przedmiotem nauczania, w planie zajec.
A wiec: "W DROGE!"
|
CWICZENIE
8 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
- nasz powyzszy przyklad moze nie byc tautologia tylko w jednym przypadku, gdy “q = 0”, a wiemy to stad, ze znamy juz matryce logiczna implikacji, ktora, bedac tu glownym spojnikiem, przyjmuje wartosc “0” dla “pierwszego czlonu = 1; drugiego czlonu = 0”. - podstawiamy wiec taka kombinacje cyfr do schematu, zakladajac, ze uczyni go to falszywym:
Zauwaz,
ze
podpisalismy
“1”
pod
symbolem
koniunkcji,
bo
to
ona
jest
glownym
spojnikiem
w
nawiasie
kwadratowym
(nasz
schemat w uproszczeniu to dwie koperty : w
lewej
znajduje sie [( q
Ale
skoro wczesniej
zalozylismy,
ze “q = 0” , trzeba nam do tego sie
zastosowac takze i teraz. Wiec
zmieniamy wartosc “q” na “0”,za “p”
podstawiamy albo “0”, albo “1”, bo
to obojetne - gdy pierwszy czlon implikacji
(mowimy teraz o tej z
okraglego nawiasu), wynosi “0” cala
implikacja jest wedlug swojej
matrycy prawdziwa, otrzymujac w ten oto
sposob zawsze falszywa
koniunkcje :
Skoro
wiemy,
ze
dla
“q
=
0”
nasza
lewa
koperta
jest
takze
zawsze
zerem,
zmieniamy
podpisy
w glownym
schemacie, otrzymujac w ten sposob taki oto
zapis :
Widzimy
teraz,
ze
z
cala
pewnoscia
badany
schemat
jest
tautologia
(przyjal
wartosc
“1”
w
obu
powyzszych
kombinacjach
zerojedynkowych). |
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Schemat, ktorego glownym spojnikiem jest rownowaznosc moze nie byc tautologia (przyjmie wartosc “0”), co wiemy z jego matrycy, jedynie w dwoch przypadkach : “pierwszy czlon = 1 , drugi = 0” oraz “pierwszy czlon = 0 , drugi = 1”, i takie tylko warianty nas teraz interesuja. - umieszczamy pod schematem takie dwie kombinacje zerojedynkowe :
Glownym
spojnikiem
pierwszego
czlonu
rownowaznosci,
znajdujacego
sie
w
lewej
kopercie,
jest
koniunkcja
wiec
to
pod
nia
podpisalismy
jego wartosci logiczne.
Czyli
podstawilismy
za
“q”
zero
i
otrzymalismy
w
okraglym
nawiasie
“1”
(wiemy
juz,
ze
gdy
pierwszy
czlon
implikacji rowna sie “0”, to cala implikacja
jest prawda i ma wartosc
“1”, bez wzgledu na to czy drugi czlon jest
zerem, czy tez jedynka).
Koniunkcja w kwadratowym nawiasie bedzie
zatem nie jedynka, jak to
wczesniej dla I-ego wariantu zerojedynkowego
zakladalismy, ale
najprawdziwszym zerem, czyniac tym samym
caly schemat prawdziwym
(podkreslona jedynka wziela sie z
rownowaznosci “0
-
teraz dochodzimy, na
podstawie
matrycy, do wniosku, ze implikacja z nawiasu
okraglego moze byc zerem
tylko w jednym przypadku dla “p” = 0.
Rezultat tego odkrycia wpiszemy
sobie pod schemat i dokonamy stosownych
dzialan:
Ku
naszemu zdziwieniu dla
“p” = 0
, “q” =1; ostatecznie okazalo sie, ze nasze
zalozenie dotyczace
mozliwosci schematu bycia falszywym,
sprawdzilo sie (podkreslone zero).
Wszystko,
co
znajduje
sie
w
klamrze
moze
teoretycznie
byc
jedynka,
jesli
:
-
lewa koperta jest jedynka
gdy
oba czlony koniunkcji sa jedynkami ( “r” =
1; “p s q” = 1).Prawy jej
czlon musi zatem byc zlozony albo z dwoch
jedynek, albo z dwoch zer, bo
tylko w takim przypadku rownowaznosc ma
wartosc “1” :
-
Umiescmy teraz w badanym
schemacie dotychczasowy wynik naszych
przemyslen :
Okazuje
sie,
ze
to,
co
wywnioskowalismy
pozwala
nam
juz
stwierdzic,
ze
nasz
schemat
nie
jest
tautologia,
bowiem juz w obu sprawdzonych kombinacjach
przyjal wartosc
“0”. Nie trzeba wiec bawic sie w dalsze
podstawianie.
Schemat,
ktorego
glowny
spojnik
to
alternatywa moze nie byc tautologia
na szczescie tylko w jednym
przypadku, gdy oba czlony sa zerami.
- implikacja
bedzie zerem, gdy “~ p” = 1, a “q” = 0 (samo
“p” jest w takim razie
zerem):
Po
umieszczeniu stosownych
wartosci w odpowiednich miejscach,
zauwazamy, ze nasza prawa koperta
przyjela wartosc “1”(jesli choc jeden
skladnik koniunkcji jest zerem, a
nasze “p” akurat teraz nim jest, cala
koniunkcja jest zerem i po jej
zanegowaniu otrzymuje sie jedynke), co
uczynilo wartosc schematu
podkreslona jedynka.
Jednak
po
podstawieniu
za
“p”
jedynki,
udalo
sie
nam
nie
otrzymac
zera
w
ramce
(wiemy
przeciez,
ze
skoro pierwszy czlon implikacji z okraglego
nawiasu ma wartosc “0”, to
cala implikacja ma zawsze wartosc “1”, bez
wzgledu na to czy drugi jej
skladnik to zero, czy jeden), bo alternatywa
“1 V 0” daje po wsze czasy
jedynke:
Wiec
schemat ten, czy to
zachodzic
go z lewej, czy tez z prawej, twardo trzyma
sie swojej jedynki i
udowadnia nam, ze jednak jest stale
prawdziwy. Tautologia, i niech mu tak
bedzie! |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
||
| Copyright (C) 1997 - 2014 by Roman Mazur |
[ przykładowe wpisy ]